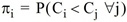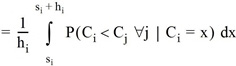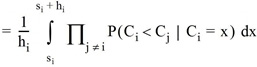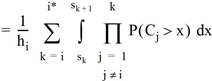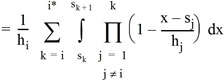Dieses Modell basiert auf der Annahme, dass ein Fahrgast nicht nur die Fahrzeiten und Takte aller Linien kennt, sondern er sich (spätestens an der Haltestelle) auch über die konkreten Abfahrtszeiten informieren kann. Im Programm wird dieses Modell verwendet, wenn Sie die Option Information an Haltestellenbereich oder Vollständige Information gewählt haben. Sie unterscheiden sich darin, ob der Fahrgast die Informationen nur am aktuellen Haltestellenbereich oder für das gesamte Netz zur Verfügung hat. Die optimale Strategie kann dann einfach wie folgt formuliert werden:
Ein Fahrgast steigt in diejenige Linie ein, deren Restkosten bei konkret gegebenen Abfahrtszeiten am geringsten sind.
Anders als in den bisherigen Fällen steigt der Fahrgast nicht einfach in die erste eintreffende Linie aus einer bestimmten (eventuell zeitabhängigen) Menge ein. Da alle Wartezeiten wi bekannt sind, unterliegt seine Entscheidung keinen stochastischen Einflüssen. Vielmehr wählt er genau diejenige Linie, deren Restkosten si + wi minimal sind.
Die optimale Linienmenge besteht also aus allen Linien, die in manchen Fahrplanlagen die geringsten Restkosten haben.
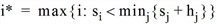und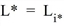 
So umfasst die optimale Menge genau diejenigen Linien, die im Grenzfall optimal sind, da sie ohne Wartezeit eintreffen, während alle anderen Linien einen vollen Takt auf sich warten lassen.
Die Berechnung der Anteile gestaltet sich in diesem Fall wie folgt:
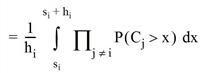[60.4]
Erläuterung der Herleitung
In Zeile [60.1] benutzt man die vollständige Information des Fahrgasts. Linie i wird genau dann gewählt, wenn ihre Restkosten Ci kleiner sind als die der anderen Linien. Zeile [60.2] formt den Ausdruck um, indem die Dichtefunktion der Zufallsvariablen Ci benutzt wird. Wegen der Konstanz der Takte ist Ci gleichverteilt in [si,si + hi). (Wird die Wartezeit mit einem Faktor gewichtet, ist dieser überall hi voranzustellen, die Rechnung ändert sich ansonsten aber nicht.)
In Zeile [60.3] nutzen wir aus, dass die Abfahrten der Linien unabhängig voneinander sind. Dies ist – in allen Wahlmodellen – eine grundlegende Annahme der taktfeinen Umlegung. Um Fallunterscheidungen zu vermeiden, wird der Integrationsbereich in [60.5] in Bereiche zerlegt, in denen das innere Produkt über eine konstante Menge von Linien erstreckt wird. Dazu muss man beachten, dass für j > k und x ∈ [sk,sk+1) zwingend P(Cj > x) = 1 gilt. Dies liegt an der eingangs getroffenen Sortierung der Linien, da die Kosten von Linie j > k mindestens sk+1 betragen. Im letzten Schritt [60.6] setzen wir schließlich die Verteilungsfunktion von Cj ein – wiederum eine Gleichverteilung. Am Ende der Rechnung steht somit eine Summe von Polynomen mit maximalem Grad i*.
Auf analoge Weise gelangt man zur erwarteten Wartezeit.
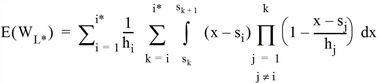
Fahrgastinformation unterstellen zu können, ist keine außerordentlich strenge Forderung. Vielerorts gibt es schon heute Informationssysteme, die die nächsten Abfahrtszeiten auf der Basis von Echtzeit-Betriebsdaten anzeigen. Alternativ können Fahrpläne an den Haltestellen ausgehängt sein. Auch anderen technischen Hilfsmitteln sind heute keine Grenzen mehr gesetzt.
